2021학년도 수능 가형 20번 어려운 이유 & 해설
2021학년도 수능 가형 20번 (by.csm).pdf
안녕하세요 CSM입니다.
20번 해설을 들고왔습니다.
현재 21번보다
체감 난이도가 높다고 여겨지는 20번입니다.
21번
체감난이도가 높은 이유는
1) 함수 g(x)의 치역설정
2) 정적분의 "결과값"을 통해 함수 개형추론
에 있어서 기존 기출에서
단단하게 연습하기 어려운 형태여서
학생들이 조금 풀기 어려워한 듯 보입니다.
먼저 교양적으로 알아야 할 사실은
아래 그림과 같이 삼각함수 반주기의
넓이(정적분값)를 빠르게 파악해야 합니다.
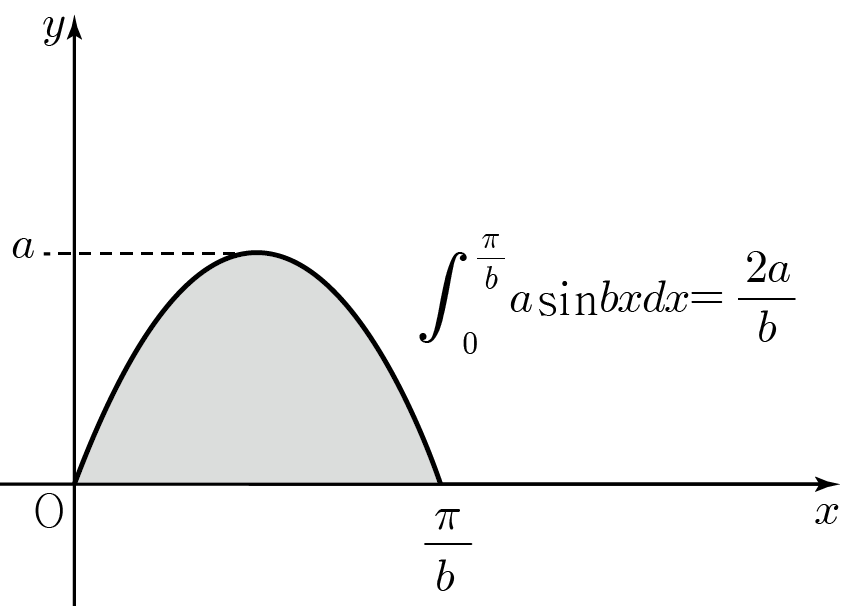
이를 토대로 해설은 다음과 같습니다. (아래 이미지 PDF도 첨부)
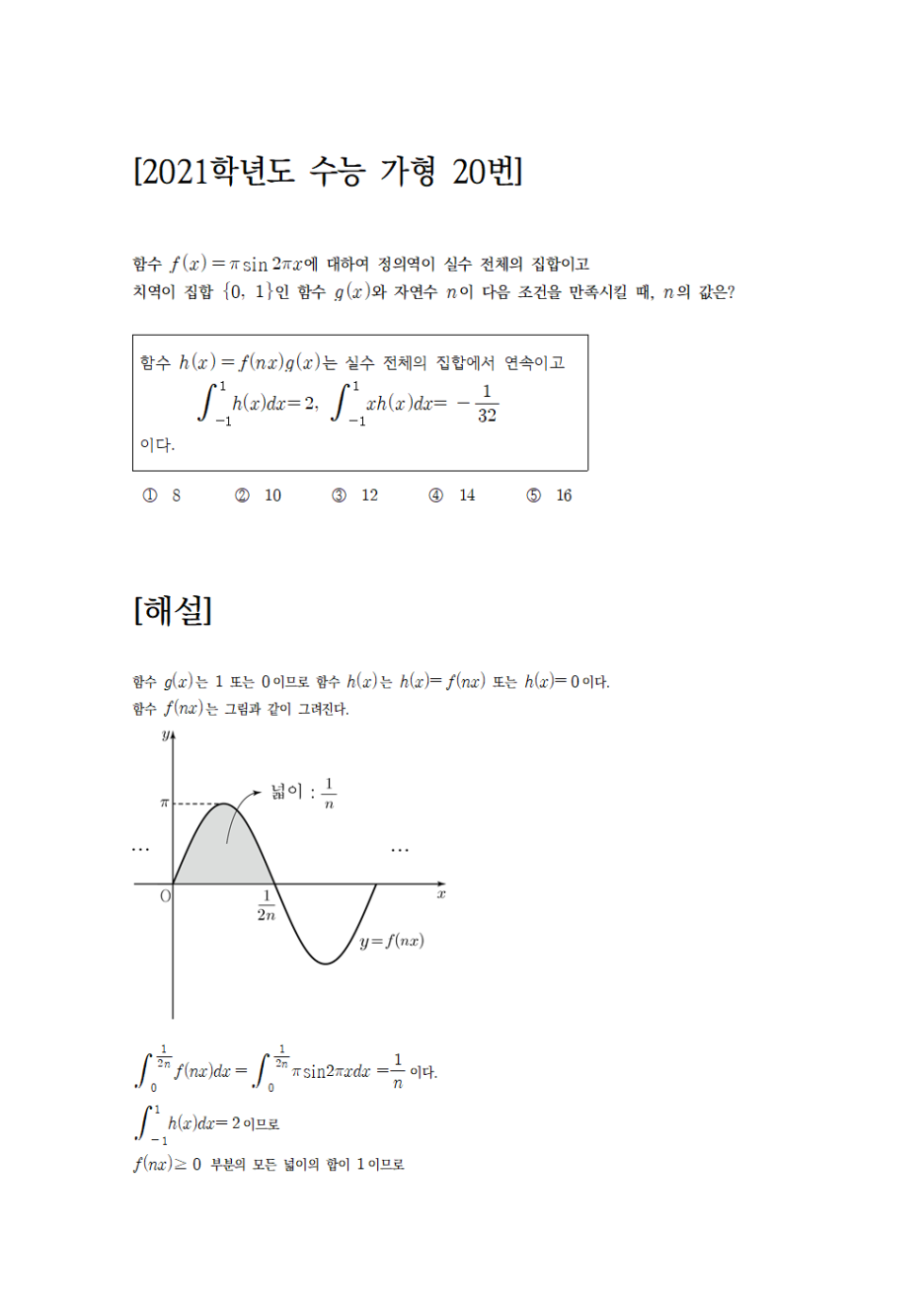
사진 설명을 입력하세요.
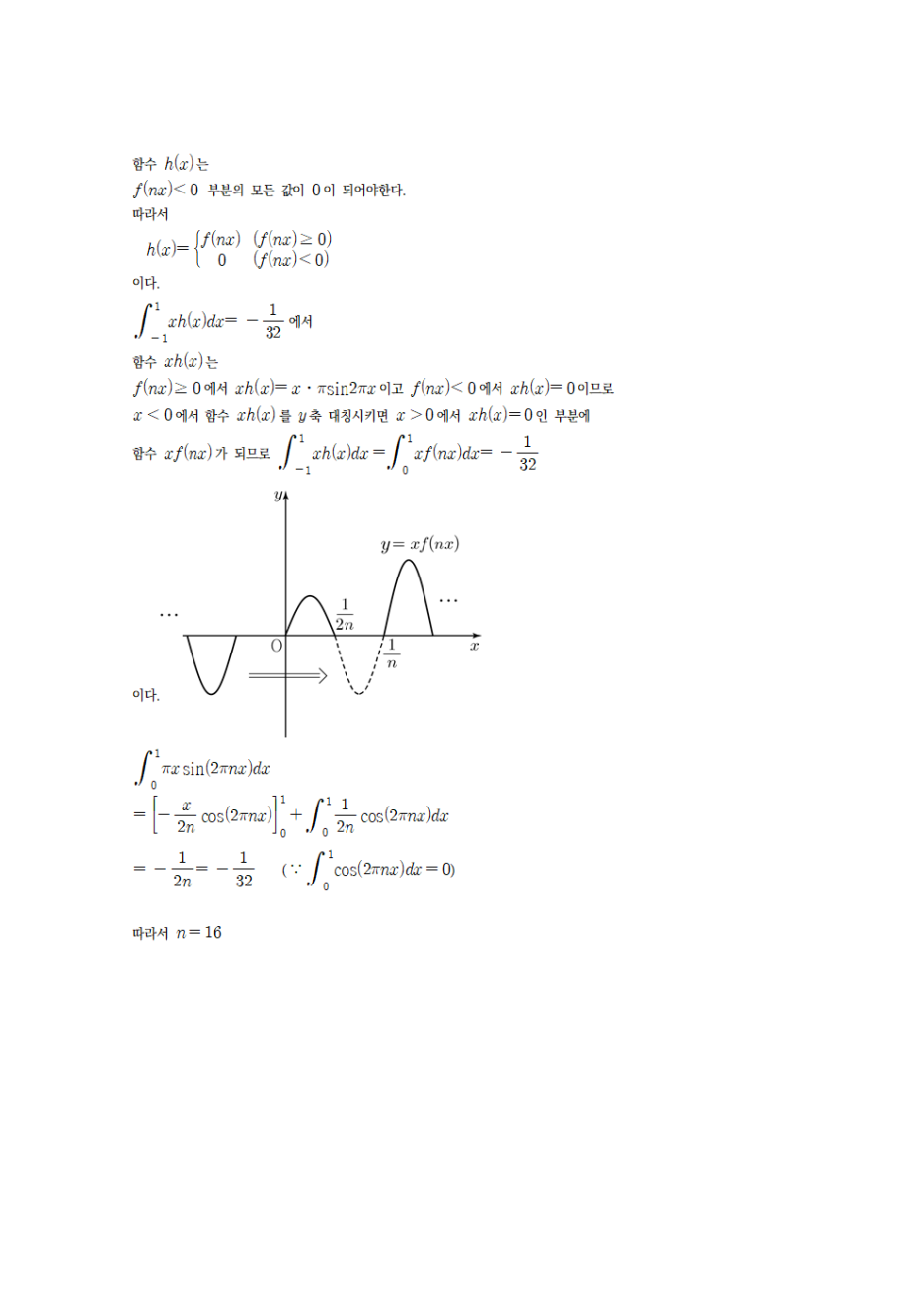
사진 설명을 입력하세요.
두가지 적분의 해석을 넓이관점과 식의 관점으로 보는 방향에 따라
풀이속도가 달라질 수 있는 문제이고 이런 경우에는
학생들에게 체감난이도 격차를 줄 수 있었던 문제라고 생각합니다.
도움이 되셨기를 바랍니다.
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-
하고 뒤적거리고 있었는데 아 공지에서 들어가면 바로 있네 아놔……
-
오르비언 중에 몇 분은 17
겸손과 주눅의 경계를 잘 모르는 것 같아요.. 너무 과하면 자기비난이 심해져요ㅜㅜ 그러지마ㅑ
-
맛집탐방이나 1
쫙 다녀야지 ㅎㅎ
-
.. 5
-
국장이 미장임...
-
흠…
-
가군 동국대 국제통상학과 5칸 추합 or식품산업관리학과 6칸 추합 나군 경희대...
-
아 연애하고싶다 1
홀로보내는 크리스마스이브라,,,, 크리스마스당일에는 알바 사장님이랑 보내네 ㅅㅂ
-
상경은 수학 높지만 성적딸려서 못가고 어문쪽은 국어반영비 높아서 못가고 끼바ㅏㅏㅏㅏㅏㅋㅋㅋㅋ
-
외대 자연계 4
외대 자연계는 다 글로벌 캠퍼스인가요?? 진학사 보니까 자연계는 한개 빼고 다...
-
국어 인강 투표 3
국어가 타 과목에 비해 많이 갈리는거같아 만들어봄(문학 독서 따로). 각 선생님...
-
냐를 갉아먹는 바퀴벌레와도 같다
-
요즘 할게없어서일본어 공부좀 시작하려는데 단어부터외우면되나요? 가타카나랑히라가나만외운수준임요
-
홍대 10명내외로 뽑는 과들 5칸뜨긴하는데 표본분석해보면 제 앞에서 이미 다 홍대...
-
전문직 아닌 이상 수능판 빨리 손절하고 자기 살 길 찾는게 답인 거 같다 서연고...
-
영어영문 제외 어문과 완전 노베이스로 가신분들 학점 따는거나 학교 생활...
-
대파라면 이거 히트네요 11
세븐일레븐 대파라면 파의 익힘 정도가 상당히 좋네요
-
잠이 안온다 0
뭘하지
-
실패 아.
-
이것 진짜 개귀찮네 의욕 뚝 떨어짐 초반인데 걍 포기하고 침대에 누움
-
돈과 여자 3
내 인생의 전부
-
취미로 공부하니 너무 재밌당><
-
일종의 급을 나눠서 자기랑은 같은 급의 대학이 아니라고 생각하는 건 당연히 있는...
-
외대 전화 추합 4
외대 논술 전화 추합은 합격증 못받나요?
-
나중에도이거때문에분명 안좋은일있을거같음 어떤방식으로든
-
수학과인데 공대를 복수전공하면 주전공 수학과 부전공 공대로 찍히는거임?
-
ㅇㅈ메타 슬슬 4
..
-
컨설팅 0
내일 컨설팅 가는데 가면 어떻게 진행되나요?!? 제가 궁금한 거 질문하는식인가요?...
-
먹다보니 괜찮군 0
괜히 욕했어
-
썩은 오이지맛
-
자라. 6
캬캬.
-
ㅁㅌㅊ??
-
이거말고는 내가치를인정받을방법이 없어서. 아닌사람들은 부러운거지
-
다시 자러감 5
ㅂㅂ
-
예비고2인데 국어학원에서 이번 수능 비문학 지문으로 수업을 하더라고요 근데 제가...
-
네당연하죠 그니까보내주세요
-
내가 보려고 정리한 재수 망한 05년생이 가능한 모든 옵션들: 0
▪︎기숙 성공가능성 High 비용 2500만원, 1년 장: 체계적인 관리, 강제성,...
-
2025 6or7월 공군 운전병 희망중인데 점수계산해보니 91점or92점입니다...
-
말이 안되는거거든요
-
정시두장밖에 못쓰는거라 너무슬퍼
-
2406이랑 올수
-
20 수능 78 100 2 97 97 22 수능 87 84 2 99 84(변명좀...
-
ㅈㄱㄴ








































개인적으로 매우 친숙한 유형은 아니라고 생각합니다. 현장기준 어려웠을 것 같아요
asinbx 한칸넓이 a/b라서 n이 2의거듭제곱만 될거같아서 1.5중에 고민하고 5번 왼쪽정적분으로 계산해보니 사인 양수는 0곱해서 없어질것같고 음수는 -1곱해져서 양수가 될것같은 느낌으로 킹리적갓심씀
ㄹㅇ 걍 찍맞이네
아니에요 킹리적갓심은 절대 그냥 나오지 않습니다. 잘하셨습니다 ^__^
해설 잘 봤어요. 마지막에 정적분 int_{-1}^{1} xh(x)dx=int_{0}^{1} xf(nx)로 넘어가는 부분이 잘 이해가 안되는데 혹시 여유있으시다면 설명해주실 수 있을까요? 저는 사진처럼 풀었는데, 계산이 무척 더럽고 현장에서 저렇게 풀면 계산실수가 반드시 있을 것 같아서 부탁드립니다....(첫 줄의 오류는 건너뛰어주세요 고치기 귀찮아서...ㅎㅎ)
in_{-1}^{0}xh(x)dx 부분만 관찰해주시면 될 것 같습니다. 함숫값이 음수인 부분은 제거 되었을것이고 양수인부분만 남은 h(x)에 대하여 x를 곱하는데 x<0이므로 xh(x)<0가 됩니다.
따라서 xh(x)를 (-1,1)에서 그린 후 각각 적분을 하여도 괜찮습니다만,
(-1,0)인 부분을 그대로 y축 대칭시켜보면 결국 xf(nx)가 완성된다는 것을 알 수 있습니다.
이는 f(nx)가 처음부터 대칭함수이고 x를 곱하여서 '대칭성질'이 남아있다고 생각하여 판단할 수 있으며 이를 (-1, 0) => (0, 1)로 이동하는 치환적분하여 식적으로도 설명가능하나 이를 계산으로 의도하기보다는 최근 "영역관찰"을 포인트 잡아왔기에 그림도 적절히 섞어서 확인해주시면 될 것 같습니다.^^
아아아아 다 그대로 대칭되니까 그렇겠네요 감사합니다.
찍는게 더 빠를 듯. 2랑 1/32 나오고 f(nx) 주기가 1/n 이니까 8, 16 처럼 2의 거듭제곱꼴로 나오는 수가 답일 것 같고 8은 너무 작아서 16했는데 아.. 계산이 엄청 빡센거였네요
진짜 시험장에서 제일 어려웠어요... 30 20 이 최고봉.
이제 21 29 은 킬러 아닌듯해여ㅜ
와.. 그냥 1/2n~1/n, 1/n~3/2n 계속 적분해가면서 귀납적으로 적분값을 찾아냈는데 y축대칭하면 한번의 적분으로 풀리네요 진짜 충격이네